Go to: Introduction, Notation, Index
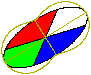
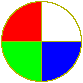
In this document 2#2 matrices are illustrated by showing the image of the unit disc under the transformation y=Ax. The disc quadrants are coloured white, red, green and blue.

The value of xTAx is plotted in polar form for x lying on the unit circle (i.e. the locus of xTAx * x is plotted). Positive values are plotted in brown and negative in cyan. When x is an eigenvector, this curve will always coincide with the edge of the disc image. The eigenvectors (if any) are plotted in brown or cyan according to the sign of the corresponding eigenvalue.
A defective n#n matrix does not have n independent eigenvectors.

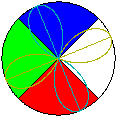


Orthogonal 2#2 matrices consist of a rotation or a reflection:
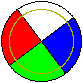
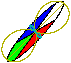

For symmetric matrices the eigenvalues and singular values have equal magnitudes and the eigenvectors lie on the axes of the disc image: