Example: Goddard Rocket (Multi-Phase)
Difficulty: Hard
This problem is an extention to the single phase roddard Rocket problem. Now, we would like to solve the problem in a multi-phase formulation, and fully alleviate the influence of singular control.
Formulate the problem in ICLOCS2
Problem definition for multiphase problem
In problem defination file GoddardRocketThreePhase.m, we can define the time variables for different phases
problem.mp.time.t_min=[0 0 0 0];
problem.mp.time.t_max=[0 70 70 70];
guess.mp.time=[0 10 20 45];the static parameters (as part of optimization variables)
problem.mp.parameters.pl=[];
problem.mp.parameters.pu=[];
guess.mp.parameters=[];and the lower bound, uppder bound and tolerance for some linear and nonlinear linkage constraints.
problem.mp.constraints.bll.linear=[0 0 0 0 0 0 0 0];
problem.mp.constraints.blu.linear=[0 0 0 0 0 0 0 0];
problem.mp.constraints.blTol.linear=[0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01];
problem.mp.constraints.bll.nonlinear=[];
problem.mp.constraints.blu.nonlinear=[];
problem.mp.constraints.blTol.nonlinear=[];Next, we need to specify different phases of the OCP as well as the corresponding settings for each phase
[problem.phases{1},guess.phases{1}] = GoddardRocket_Phase1(problem.mp, guess.mp);
[problem.phases{2},guess.phases{2}] = GoddardRocket_Phase2(problem.mp, guess.mp);
[problem.phases{3},guess.phases{3}] = GoddardRocket_Phase3(problem.mp, guess.mp);
phaseoptions{1}=settings_GoddardRocketThreePhase_Phase1(10);
phaseoptions{2}=settings_GoddardRocketThreePhase_Phase2(10);
phaseoptions{3}=settings_GoddardRocketThreePhase_Phase3(10);In the linkage constraint function bclink, we can define the linkage constraint equations as
blc_linear=[xf{1}(1)-x0{2}(1);xf{1}(2)-x0{2}(2);xf{1}(3)-x0{2}(3);xf{2}(1)-x0{3}(1);xf{2}(2)-x0{3}(2);xf{2}(3)-x0{3}(3);tf(1)-t0(2);tf(2)-t0(3)];
blc_nonlinear=[];Problem definition for individual phases
First, the problem definition for the individual phases can be specified following the same formulation as for single-phase problems. For this particular example, we generated the following files
- GoddardRocket_Dynamics_Phase1.m: same as GoddardRocket_Dynamics_Internal.m
- GoddardRocket_Dynamics_Phase2.m: same as GoddardRocket_Dynamics_Internal.m, with one additional path constraint from the singular arc condition
term1=T-D0.*v.^2.*exp(-h/H)-m*grav; term2=-m*grav./(1+4*(c./v)+2*(c^2./(v.^2))); term3=(c^2/H/grav.*(1+v./c)-1-2*c./v); sarcconst=term1+term2.*term3; g_eq=[sarcconst]; - GoddardRocket_Dynamics_Phase3.m: same as GoddardRocket_Dynamics_Internal.m
- GoddardRocket_Phase1.m: same as GoddardRocket.m, with minor differences. The main ones are for the time variables
for static parameters,
% Initial time. problem.time.t0_idx=1; problem.time.t0_min=problem_mp.time.t_min(problem.time.t0_idx); problem.time.t0_max=problem_mp.time.t_max(problem.time.t0_idx); guess.t0=guess_mp.time(problem.time.t0_idx); % Final time. Let tf_min=tf_max if tf is fixed. problem.time.tf_idx=2; problem.time.tf_min=problem_mp.time.t_min(problem.time.tf_idx); problem.time.tf_max=problem_mp.time.t_max(problem.time.tf_idx); guess.tf=guess_mp.time(problem.time.tf_idx);for input variables,% Parameters bounds. problem.parameters.pl=problem_mp.parameters.pl; problem.parameters.pu=problem_mp.parameters.pu; guess.parameters=guess_mp.parameters;for the data storage static parameters, add additionally% Input bounds problem.inputs.ul=[T_max]; problem.inputs.uu=[T_max]; % Bounds on first control action problem.inputs.u0l=[T_max]; problem.inputs.u0u=[T_max]; % Input constraint error bounds problem.inputs.uConstraintTol=[0.1]; % Guess the input sequences with [u0 uf] guess.inputs(:,1)=[T_max T_max];and in the Mayer cost function E_unscaledproblem.data=problem_mp.data;boundaryCost=0; - GoddardRocket_Phase2.m: same as GoddardRocket.m, with minor differences. The main ones are for the time variables
for static parameters,
% Initial time. problem.time.t0_idx=2; problem.time.t0_min=problem_mp.time.t_min(problem.time.t0_idx); problem.time.t0_max=problem_mp.time.t_max(problem.time.t0_idx); guess.t0=guess_mp.time(problem.time.t0_idx); % Final time. Let tf_min=tf_max if tf is fixed. problem.time.tf_idx=3; problem.time.tf_min=problem_mp.time.t_min(problem.time.tf_idx); problem.time.tf_max=problem_mp.time.t_max(problem.time.tf_idx); guess.tf=guess_mp.time(problem.time.tf_idx);for boundary constraint,% Parameters bounds. problem.parameters.pl=problem_mp.parameters.pl; problem.parameters.pu=problem_mp.parameters.pu; guess.parameters=guess_mp.parameters;for the data storage static parameters, add additionallyproblem.constraints.bl=[0 0.1]; problem.constraints.bu=[0 inf]; problem.constraints.bTol=[0.1 0.1];in the Mayer cost function E_unscaledproblem.data=problem_mp.data;and in the Boundary constraint function b_unscaledboundaryCost=0;ht0 = x0(1); vt0 = x0(2); mt0 = x0(3); H = vdat.H; D0 = vdat.D0; grav = vdat.grav; c = vdat.c; bc=[mt0*grav-(1+vt0/c)*D0*vt0.^2*exp(-ht0/H);tf-t0]; - GoddardRocket_Phase3.m: same as GoddardRocket.m, with minor differences. The main ones are for the time variables
for static parameters,
% Initial time. problem.time.t0_idx=3; problem.time.t0_min=problem_mp.time.t_min(problem.time.t0_idx); problem.time.t0_max=problem_mp.time.t_max(problem.time.t0_idx); guess.t0=guess_mp.time(problem.time.t0_idx); % Final time. Let tf_min=tf_max if tf is fixed. problem.time.tf_idx=4; problem.time.tf_min=problem_mp.time.t_min(problem.time.tf_idx); problem.time.tf_max=problem_mp.time.t_max(problem.time.tf_idx); guess.tf=guess_mp.time(problem.time.tf_idx);for input variables,% Parameters bounds. problem.parameters.pl=problem_mp.parameters.pl; problem.parameters.pu=problem_mp.parameters.pu; guess.parameters=guess_mp.parameters;and for the data storage static parameters, add additionally% Input bounds problem.inputs.ul=[T_min]; problem.inputs.uu=[T_min]; % Bounds on first control action problem.inputs.u0l=[T_min]; problem.inputs.u0u=[T_min]; % Input constraint error bounds problem.inputs.uConstraintTol=[0.1]; % Guess the input sequences with [u0 uf] guess.inputs(:,1)=[T_min T_min];problem.data=problem_mp.data; - settings_GoddardRocketThreePhase_Phase1.m: same as settings_GoddardRocket.m, but only contains phase depended settings
- settings_GoddardRocketThreePhase_Phase2.m: same as settings_GoddardRocket.m, but only contains phase depended settings
- settings_GoddardRocketThreePhase_Phase3.m: same as settings_GoddardRocket.m, but only contains phase depended settings
Main script main_GoddardRocketThreePhase.m for solving the multi-phase Goddard rocket problem
Now we can fetch the problem and options, and solve the resultant NLP.
options.mp= settings_GoddardRocketThreePhase; % Get options and solver settings
[problem,guess,options.phaseoptions]=GoddardRocketThreePhase; % Fetch the problem definition
[solution,MRHistory]=solveMyProblem( problem,guess,options);Results from ICLOCS2
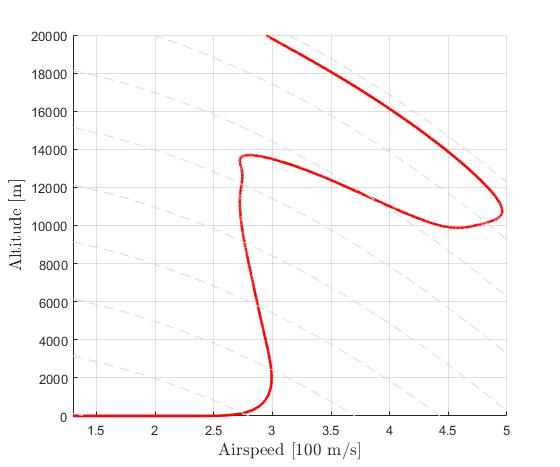
Using the Hermite-Simpson discretization scheme of ICLOCS2, the following state and input trajectories are obtained under a mesh refinement scheme starting with 10 mesh points for each phase. The computation time with IPOPT (NLP convergence tol set to 1e-09) is about 2.5 seconds, using finite difference for derivative calculations on an Intel i7-6700 desktop computer.
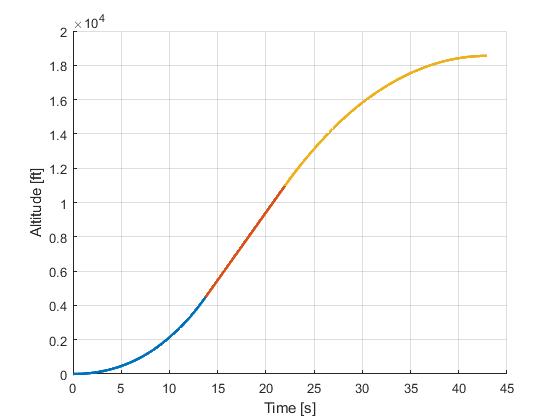
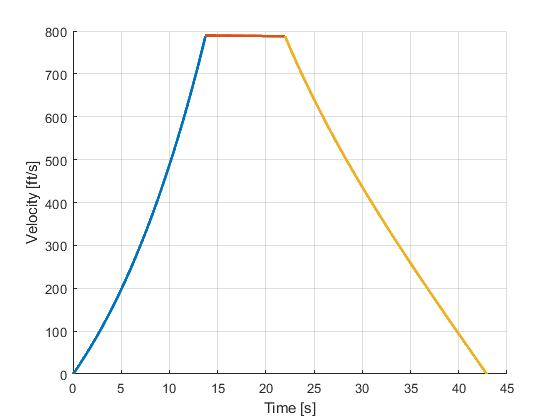
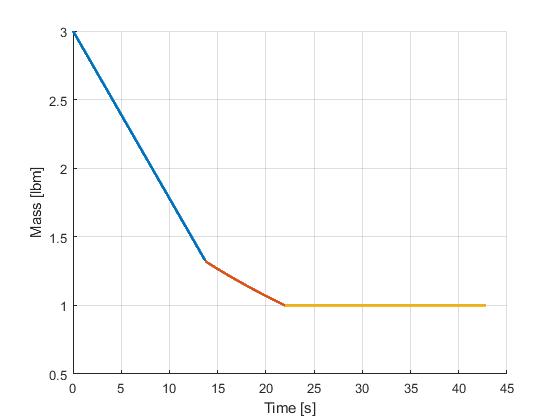
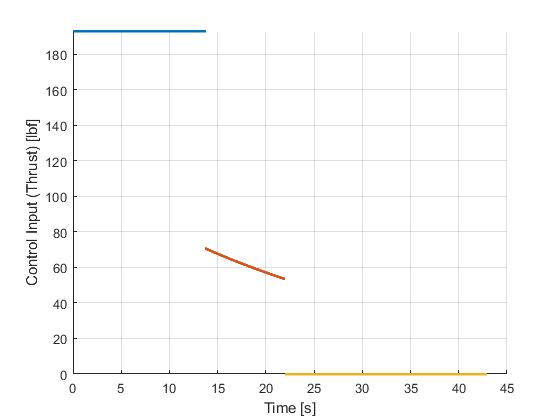
[1] J. Betts, "Practical Methods for Optimal Control and Estimation Using Nonlinear Programming: Second Edition," Advances in Design and Control, Society for Industrial and Applied Mathematics, 2010.