Example: Second Order Singular Control Problem
Difficulty: Easy
This problem was originally presented by [1], with the challenge of being a singular control problem. This example is available via the link on the right.
The implementation of this examples will not be explained in details due to similarity with other examples. Please refer to an example with similar complexity for implementation instructions, or other examples in the list of examples with Detailed Instructions.
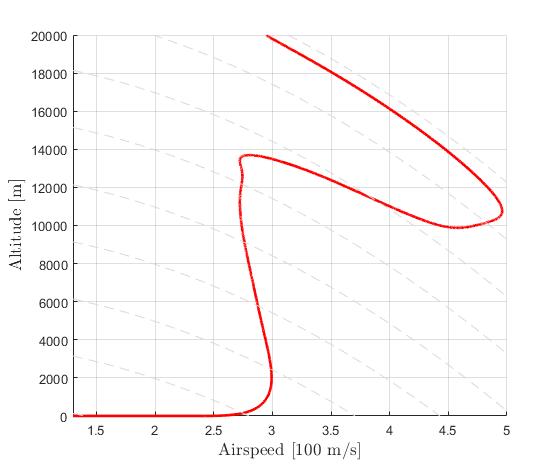
Results from ICLOCS2
The original presentation of the problem will lead to singular control. However, upon noticing that the dynamic equation
is essentially to impose a rate constraint on the velocity state (x_dot). We can reformulate the problem with x_dot now an input variable with input rate constraint [-1,1], aiming to allivate the influence of singular control.
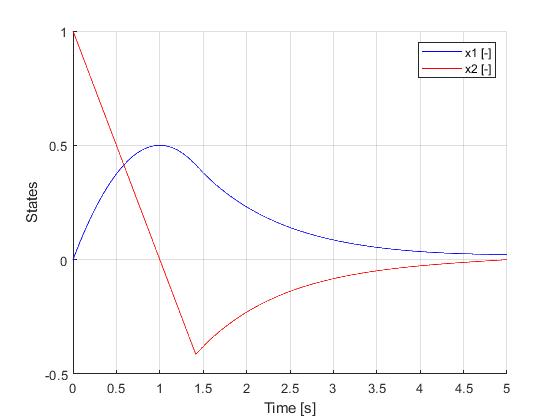
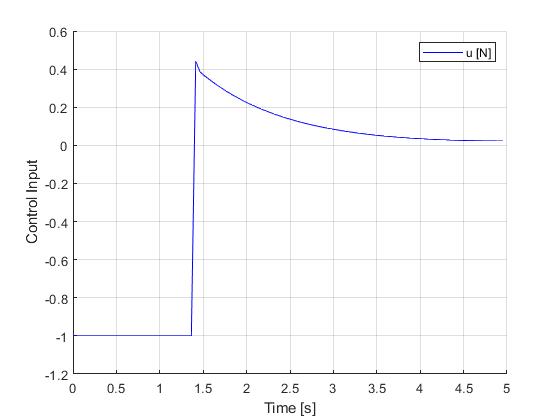
Using the Hermite-Simpson discretization scheme of ICLOCS2, the following state and input trajectories are obtained using an uniform mesh with 99 intervals, with direct collocation method and IPOPT (NLP convergence tol set to 1e-09). No influence of singular arc can be observed.
[1] G.M. Aly. 1978. The computation of optimal singular control.Internat. J. Control28, 5 (1978), 681–688.