ICLOCS2

We can specify the system dynamics in function Hypersensitive_Dynamics_Internal with

dx=-x.^3+u;

For this example problem, we do not have any path constraints, so function Hypersensitive_Dynamics_Internal only need to return the value of variable dx .

Similarly, the (optional) simulation dynamics can be specifed in function Hypersensitive_Dynamics_Sim.m .

First we provide the function handles for system dynamics with

InternalDynamics=@Hypersensitive_Dynamics_Internal;
SimDynamics=@Hypersensitive_Dynamics_Sim;

The optional files providing analytic derivatives can be left empty as we demonstrate the use of finite difference this time

problem.analyticDeriv.gradCost=[];
problem.analyticDeriv.hessianLagrangian=[];
problem.analyticDeriv.jacConst=[];

and finally the function handle for the settings file is given as.

problem.settings=@settings_Hypersensitive;

Next we define the time variables with

problem.time.t0_min=0;
problem.time.t0_max=0;
guess.t0=0;

and

problem.time.tf_min=10000;
problem.time.tf_max=10000; 
guess.tf=10000

For state variables, we need to provide the initial conditions

problem.states.x0=1;

bounds on intial conditions

problem.states.x0l=1; 
problem.states.x0u=1; 

state bounds

problem.states.xl=-inf;
problem.states.xu=inf; 

bounds on the absolute local and global (integrated) discretization error of state variables

problem.states.xErrorTol_local=1e-7; 
problem.states.xErrorTol_integral=1e-7;

tolerance for state variable box constraint violation

problem.states.xConstraintTol=1e-7;

terminal state bounds

problem.states.xfl=1.5; 
problem.states.xfu=1.5; 

and an initial guess of the state trajectory (optional but recommended)

guess.states(:,1)=[0 0]; 

Lastly for control variables, we need to define simple bounds

problem.inputs.ul=-inf;
problem.inputs.uu=inf;

bounds on the first control action

problem.inputs.u0l=-inf;
problem.inputs.u0u=inf; 

tolerance for control variable box constraint violation

problem.inputs.uConstraintTol=1e-7; 

as well as an initial guess of the input trajectory (optional but recommended)

guess.inputs(:,1)=[0 0];

Since this problem only has a Lagrange (stage) cost , and no Mayer (boundary) cost ,we simply have

stageCost = 0.5*(x.^2+u.^2);

boundaryCost=0;

for sub-function L_unscaled and E_unscaled respectively.

For this example problem, we do not have additional boundary constraints. Thus we can leave sub-routines b_unscaled as they are.

Now we can fetch the problem and options, solve the resultant NLP, and generate some plots for the solution.

[problem,guess]=Hypersensitive;          % Fetch the problem definition
options= problem.settings(1,8);                  % for hp method
% options= problem.settings(40);                  % for h method
[solution,MRHistory]=solveMyProblem( problem,guess,options);
[ tv, xv, uv ] = simulateSolution( problem, solution, 'ode113', 0.01 );

Note the last line of code will generate an open-loop simulation, applying the obtained input trajectory to the dynamics defined in Hypersensitive_Dynamics_Sim.m , using the Matlab builtin ode113 ODE solver with a step size of 0.01.

Using the hp-LGR discretization scheme of ICLOCS2, the following state and input trajectories are obtained under a mesh refinement scheme starting with 1 mesh interval with polynomial order of 8. The computation time with IPOPT (NLP convergence tol set to 1e-09) is about 1 seconds for 4 mesh refinement iterations together, using finite difference derivative calculations on an Intel i7-6700 desktop computer. The final mesh have 43 intervals with polynomial orders ranging from 3 to 8. Subsequent recomputation using the same mesh and warm starting will take on average 0.1 seconds and about 3 iterations.

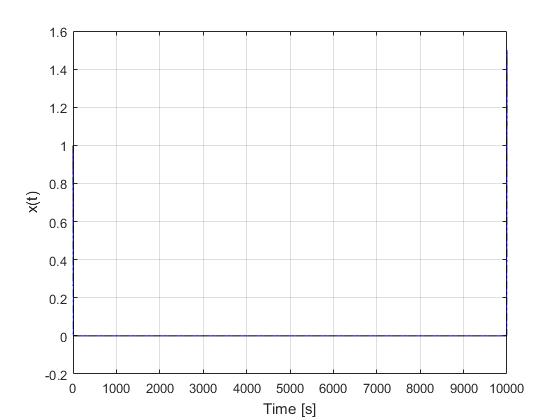
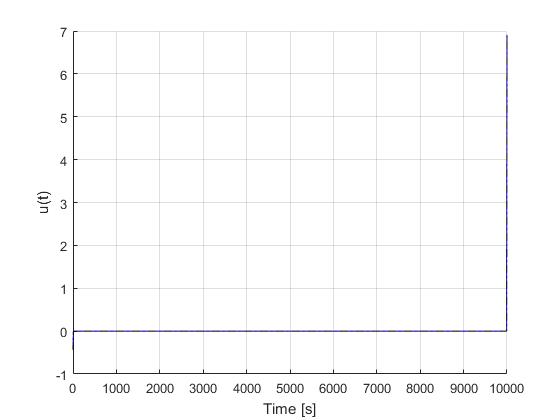
It is interesting to note that if this problem is to be solved without the mesh refinement scheme using equally spaced mesh, even 1000 grid intervals with the same polynomial order can only bring down the maximum absolute local error to 0.6273, far larger than the required 0.0000001. The computation time in this case is about 15 seconds (14900% higher). This clearly demonstrated the benefit and necessity of mesh refinement .